Analytic Techniques
Common Patterns in Raster Modeling
This tutorial introduces several useful tools and patterns for using raster GIS data and procedures. In previous tutorials we have looked at the language of relational data models that represent entities as collections of attributes stored as rows in tables. Relational databases provide a collection of tools (structured query language) that allow us to represent and explore relationships between these entities. Vector GIS extends relational databse functions with spatial data types and spatial functions. These allow us to explore spatial relationships like proximity or overlap.
The vocabulary of vector-relational GIS is categorical in nature. The entities represented are singular and discrete. For many purposes the chunkification of the world can be helpful. For example it can be helpful to think of a transit stop as a point or a property parcel as a polygon.
We have also looked at raster / cell-based data like terrain models and imagery we downloaded from the U.S. Geological Survey. While vector data models attempt to represent discrete features, raster datasets represent "locations" in a layer of congruent cells. These layers are suited to representing phenomena that vary in a smooth, continuous fashion from one location to another. There are many aspects of the landscape that are more conveniently modeled as raster layers. Examples include: Elevation, and its derivitive, slope; diffuse phenoena such of sound or air polution, cumulative costs associated with traveling over the landscape, and many more. Rasters can also represent categorical phenomena like land use or census geography. Disintegrating these lumpy features into cells facilitiates exploration the juxtaposition of conditions on a cell-by-cell basis. Raster and Vector data models and analytical techniques are both important tools for people concerned with spatial problems. It is not uncommon to have GIS analyses that use both Raster and Vector procedures.
Sample Dataset
- Click here to download the zip archive of the sample dataset Open the file StarTutorialHere.mxd.
- Spatial Models for Scholarship and Decistion Support
- Geoprocessing Cheat Sheet
Like Vector-Relational GIS has its language of logical operators for filtering, transforming and associating enitities represented in tables. Raster GIS has a similar family of procedures that are much different from SQL. C. Dana Tomlin is credited for describing (if not inventing) this language of tools in the early 1980s in a software package named the Map Analysis Package. Whereas SQL can be said to be the offspring of set theory, Tomlin's language for Cartographic Modeling takes its metaphor from map overlays. Because it is a language of functions that treat map layers as inputs and outputs, and that create new map layers as outputs these techniques are sometimes known as Cartographic Modeling, The term Map Algebra is also sometimes used.
A Functional Vocabulary of Rasters and Map Algebra
In map algebram the fundamental building block of representation is a cell that represents a localtion having some attribute (a value). Cells in a raster layer having the same value are known as a zone. Tomlin described four basic families of functions that allow you to derive new raster layers as functions of existing layers. The Raster Demo toolbox in the sample datset provides an example each of these function types. For a deeper description of the functional vocabulary of rasters and map algebra, see these illustrations of the basic vocabulary of rasters and map algebra.
Using the Demo Dataset
This tutorial provides several geoprocessing models that demonstrate the most common patterns in using rasters. To use the tutorial, download the sample dataset, linked above, and open the models in the pbc_Raster_Demo toolbox, open each of the models in edit mode and run each of the procedures from top to bottom. To understand how the models work you can expose the help panel and explore the context-sensitive descriptions of parameters and visit the help documentation for each function. After running each function you should explore the outputs that are created. You may also find it useful to alter the models by adjusting the parameters. You may even want to make copies of some of the models before making major modifications. Finally, you can copy the raster Demo toolbox to your own project and use the models as a starting place for your own analyses.
Set up Your Tools and Scratch Folder and your Geoprocessing Environment
We are about to develop a sequence of analytical operations that we want to save as Geoprocessing models. This mode of creating re-usable models wil allow us to easiy refine and esperiment with different values and priorities once we have the model running. Our sample dataset has Tools and Scratch Folders set up within our project folder. and and the Geoprocessing Environment has been set up on our sample map document. When you set up your own project, you will want to consult the Geoprocessing Cheat Sheet for tips on how to do this.
Important! Set Processing Extent. The default behavior of many rster tools will be to create a new raster that has the same extent as the input data. This can result in creating a new raster that is either too broad -- leading to an excess of time being spent waiting for things to process. Or the extent may be too narrow, suach as what would happen if you try to comput distance from one or two points, the extent of the result would be clipped to the extent of the points, which might actually cover no area at all. For the demonstration that follows, you should se the Geoprocessing Environment Variable or Processing Extent to be the same extent as the layer Large Study Frame.Setting the procesing extent in every map document is a good habit when working with rasters. But you should also be aware that once this ebvironment variable is set, it can cause unexpcted behavior -- for example when using Select By Location or Select By Attributes m,ay not select features that are outside of this extent.
Cartographic Modeling
The five models inside the Cartographic Modeling toolset will demonstrate a larger pattern of weighted map overlay analysis that is sometimes known as McHargian Overlay named for Ian McHarg who popularized the technique (using acetate and magic markers) in his 1961 book, Design with Nature. The computer version of this method was described by Dana Tomlin in Cartographic Modeling. The process involves the creation of layers with cell values that are evaluated with regard to some application-specific criteria: such as "Too Steep for Building." These cell values are typically integer numbers that are normalized to some scale. After modeling several individual criteria, then composite layers can be made by adding up the scores at each cell -- assigigning these values to cells in a new raster. The easiest way to do this is to normalize the scores for each criteria to a common scale, for example:
- 3 = Best
- 2 = Good
- 1 = OK
- 0 = Not particularly good but might be ok if other conditions are excellent.
- -1 = Costly remediation required
- NoData = Absolutely not. Never.
At the end, these layers can be added up with weights applied to create a Suitibility Map. The sutibility map can be used to turn conceptual models into maps that reveal patterns that would not be obvious at all in an aerial photograph or on the ground. These maps can provide insights into ways that the landscape works and can also be used for prioritizing areas for attention or for planning or simply for discussion. At the end of our demonstration you will also see how these spatial functions can be used to evaluate current conditions and to think strategically about priorities.
What Makes a Good Hub Library?
The new library director is exploring a new conceptual model of the library system that would involve Hub libraries and Branch Libraries. Hubs are near commercial areas and stops on the light rail system. Branches are in areas that have a high density of residents. Our demonstration will use three new types of map algebra functions to explore the three conceptual phenomena.
Aside... Experimenting with Alternative Futures
While this tutorial is about libraries, you may want to make a model that evalustes the alternative locations of other sorts of things and conditions: Locations of food stores and convenience stores, for example, or pet-oriented services, or linear facilities, like new links in a network of bicycle trails, or a polygon representing a new habitat preserve..
The Tutorial Creating A Feture-Class to Represent Existing Conditions and Alternative Futures provides a method for creating a feature-class to support such what-if studies.
A fun and semi-challenging brain-teaser would be to use our hub-library site suitibility model to evaluate the locations of existing libraries. If you decided to include a new sub-model to consider duistance from existing libraries how could you use your experimental frame to explore the possibility of removing an existing library and adding a new one. Hint: the tricy part is that all existing libraries are by definition 0 meters from themselves...
A Distance Function
There are many map algebra functions that create continuous functions. Many of these use models of diffusion -- like values increasing or diminishing with distance from some features or zone. The Euclidean Distance function is the simplest example. More elaborate variations can explore the effect of interference that is represented in a cost map layer. The visibility functions are a variation on these functions that you could say act by incremental spread and evaluation.
References
- The Euclidean Distance function is located in the ArcGIS geoprocessing toolbox in the Spatial Analyst / Distance toolbox.
- The Reclass tool is located in the Spatial Analyst / Reclass toolbox.
The Transit Distance model witin the Cartographic Modeling toolset uses a euclidean distance function and a reclass function to create a new map whose cell values represent the crow-flight distance, in Meters) from each transit stop. We then use a Reclass function to transform the function from units of meters into a simple four-class normalized value system. The Reclass function is one of the most important functions in cartographic modeling. Reclass fuunction allows you to assign new integer values to locations based on ranges of values in an input raster.
References
- The Reclass tool is located in the Spatial Analyst / Reclass toolbox.
- The The Polygon to Raster tool is located in the Conversion tools / To Raster toolbox.
Rasterize and Reclass Land Use
Our concept of Hub libraries includes a preference for areas of heavy daytime traffic. This would be commercial an institutional areas. In consideration of existing land use, residential areas may also be a good context. IOther types of land use are not necessarily preferred or avoided. But others, such as open water or wetlands are absolutely ruled out.
The Land Use Sutibility model begins by turning the polygon features from the MassGIS 1999 Land Use layer into a raster. The heart of this function is the identification of a feature attribute that will determie the values of the cells in the output. In this case we are using the values of LU21_1999 You can explore the data dictionary in the metadata, linked above to see how we assign our normalized values to individual cell values and ranges. Take a look at the cell-size parameter of the Feature to Raster function and the run it and inspect the output layer in terms of its faithfulness to the original. For a deeper ediscussion and diagrams about evaluating cell-size in categorical and continuous rasters can be found in the Digital Elevation Models tutorial.
NoData: Creates Voids
The other important thing to notice here is the use of the NoData value. NoData creates a void in the map that is useful for a couple of reasons. The voids created by NoData values over-ride any other values in a cartographic model. So they allow you to represent Absolutelu Not in an multiparametric overlay.
The voids created by NoData also provide the context for incremental functions like Euclidian Distance or cost distance.
Focal, Neighborhood Functions
The next relationship in our concept of Hub Libraries has to do with the density of the neighborhood. This is tricky because our best represntation of density comes from census data that is aggregated at a block level. But since we think that patrons would be happy to walk up to 500 meters to come to the library, simply evaluating the population density of the block that a library is in would not capture the relationship. Using larger aerial units like block groups or tracks is a bad idea because libraries are likely to be near the edges of these places that are often bounded by major roads.
Take a look at the Neighborhood Density model to see how we transform the census blocks into a raster that estimates a count of residents that might live at each 10 meter cell. There are a lot of steps here. It will be besst for you just to look at the model than for me to try to explain this in words.
References
- The Focal Statistics tool is located in the Spatial Analyst / Neighborhood toolbox.
ALERT!! The Focal Statistics tool has problems using or creating rasters in any format other than ArcInfo GRID. Normally we prefer to create our inoputs and outputs in Imagine .img format. The Focal Statistcs tool does useless and confusing things unless the Input Raster and the Output Raster are in GRID format. To accomplish this, simply leave off the .img suffix in whaterver tool has created the input for Focal Statistics, and leave off the .img suffix when naming the Output Raster when you set up the Focal Statistics tool.
Inscruitible bugs like this one used to be a lot worse with ArcGIS. You still run into them here and there. Some tools require that all inputs are in the same projection. Others only want integer rasters as inputs. Some tools refuse to work on datasets that are in folder names that have spaces, or funny characters in their names. Usually discovering what is wrong requires you to isolate the procedure that is not working, and build new, very controlled workspace, and a new mxd document, then just start toggling all of the options.
It should go without saying that you don't want to be working on a needlessly huge data-set while you are trying to cycle through problems as quickly as possible. In fact. the process of creating a small sample dataset to experiment on is a good first step, which might reveal whether a corrupt input raster might be the problem.While you are performing this arcmap excorcism, also begin thinking of ways that you can work around this stupid broken tool. By the time you have exhausted all of the possible things you might be doing wrong, you will have discovered how to satisfy the tool or figured out some other combination of tools that wil do the job.
When you get really desperate, it is customary to offer flattery to Saint Jude, and name your files in her honor. It also would be a good idea to report your bugs to ESRI technical Support. If you are reporting a new bug that they don't already know about, they may ask you to provide a zipped archive your little experimental debugging laboratory with the sample data and mxd and a demo-model all referring to eachother with relative path names.
The new raster created by the Focal Statistics has cell values that repreent the estimated count of residents living witin 500 meters of each location.
Overlay with the Map Calculator
The essence of Map Algebra becomes clear when you look at the Map Calculator function in the Hub Library Suitibility model. This model returns a composit score for each location on the map by weighing the values in the value layers we created in the three preceding models.
References
- The Raster Calculator Tool is located in the Spatial Analyst / Map Algebra Toolbox .
An unweigted map algebra expression (see below) produces a new composite score by adding together equally-weighted scores for individual criteria and dividing the sum of individual scores by the number of individual scores. This last step normalizes the resulting composite score so that it is in the same standardized range of values as everythign else. for example:
HubLibraryScore.img = (TransitScore.img + LandUseScore.img + DensityScore.img) / 3
It is often the case that a model of this kind may end up recommending to broad an area as "Top Priority." In such cases you may want to g back and adjust the reclass values in your individual models, or you can also change the weights of the individual scores by simply adding positive and negative factors to them, as depiced below:
HubLibraryScore.img = (TransitScore.img + LandUseScore.img + (2 * DensityScore.img)) / 4
Notice how the weighting expression is enclosed in parentheses, and the 4 in the denominator of the above expression is the sum of the weights. Unweighted terms having the implicit weight of 1..
Weighting is simplest using integer scores and integer weights. If all of the input rasters or weighting factors used in a map algebra expression are integers, the result wil be an integer, If any of the above involve deciimals, then the result is likely to have decimal places as well. And this may be OK. If not. Then you can round individual expressions or the result, using the inf() function.
A Local Function: Evaluate Each Existing Library.
Our first two models demonstrate a couple of ways of moving information from the raster world of surfaces to the vector world of discrete objects represented in tables. The first example, Extract Value by Point looks at how you can use a surface, elevation in this case, to create new values in a table of points. Try this model to see how we can augment the massGIS libraries layer to add an elavation value to each library. We will return to this function at the end of this tutorial to see how it can be used to evaluate point locations based on surfaces that we create.
h3>References- The Extract Value by Point tool is located in the Spatial Analyst / Extraction Toolbox .
This model introduces a couple of useful geoprocessing patterns...
Create a New Layer Before Joining
The Sample function creates a new table of elevations for each point. The final step wil lbe to join this sample table back to the libraries layer. IN anticipation of this join we begin by selecting the libraries within our study frame and saving this selected set to a new layer. This new layer provides a table to join to. Take a look at the Source Properties for th enew layer to see that this layer referencesthe original massGIS libraries shape file. It is a virtual view that is part of our ArcMap document. This pattern is useful because the view is wiped out each time we run our model. This pattern avoids problems that occur when you use a model to join to original input layers. The problem comes up when you re-run the model and it will see that the layer has already been joined.
To understand how the join is made you ought to open up the attribute tables for the Study Area Libraries Layer and the Library Elevation table to see which columns are used in the join. It is not obvious at first which columns should be used to join these tables, but after sorting the tables a couple of different ways, you can see that the FID in the Libraries table corrresponds with the LIBRARIES_ column in the sample table.
After running this model take a look at the attribute table for the Study Area Libraries layer. See that we now have a value for elevation for each of the libraries.
Reproject Before Using
Up until now, we have enjoyed a care-free way of working with data-sets that are in different coordinate systems. When you add data to ArcMap, If the layer has its coordinate referencing system properties, ArcMap will transforms the data-set so that it aligns with the coordinate system of the data frame. Most vector tools, like Buffer and Near and Spatial Joins deal input data in varioua geographic or projected coordinate systems, and wil predictably transform the inputs according to the Geoprocessing Environment Setting for Output Coordinates. So we should br grateful for that!
Now as we enter the world of raster tool-kit this project-on-the-fly mechanism is not as reliable. For example, EuiclideanDistance tool (and others, I have noticed) only work correctly if the input data is in the same coordinate system as the environment setting for Output Coordinates (OCS). The great sin of ArcMap is that the tool ought to be able to see that this mismatch is occurring, and stop with some meaningful warning. Instead, it simply acts like nothing is wrong and creates an output that is clearly useless. So the ArcMap honeymoon is over. Welcome to the ArcMap hater's club.
If you find that raster tools aren't working, check the coordinate system properties of the input data-set by double-clicking on it in the Table of Contents, and inspect the General tab. If you scroll down, you wil find the projection definition. If the data difers from the Output Coordinates environement setting, there are a couple of ways that you can reproject your data before using it in a geoprocessing model. The model. 1. ReprojectBeforeUsing, in the pbc_Raster_Demo toolbox shows a couple of modeling patterns that will make sutre that your features are in the right coordinate system. The euclidean distance function is includes in this model just as an example.
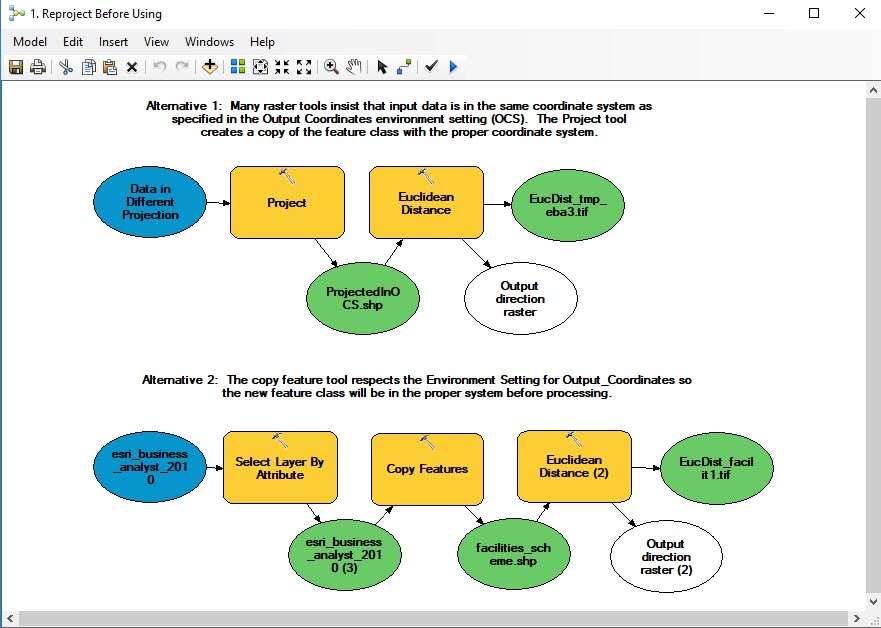
The Project tool can be found in the Data Management > Projections and Transformations toolbox.
It is natural to be annoyed by this sort of thing. On the other hand, it is a patchwork of a huge number of tools that have been developed in different coding frameworks over a 30 year period, therefore, some parts are more user-friendly than others. For old-school ArcGIS users can tell you how awful it was back in the old days.,.
A Zonal Function to Summarize Surface Information to Polygons
The model Summarize Surface over Polygons uses a zonal function to summarize elevation values from our USGS elevation model for each census block group. THis model allows us to explore the question of whether there is any relationship between elevation and median block group income. This model uses the same create-layer-then-join pattern described fo rthe previous model.
Scatter Plots
At the end of this model we join the resulting zonal statistics table to our layer of study area blockgroups then convert these blockgroups to points. The reason for this is that we want to make a scatter plot out of the points. The ArcMap Graph tools are very cool. We can make a scatter plot of points to explore the relationship of elevation with median block group income. When the scatter plot is finished we can select points from regions of the plot to see where these cases are on the map! Notice that making a thematic map from the points
Two Interpolation Methods Kernel Density vs Focal Sum
The kernel density function creates what are commonly referred to as Heat Maps. A more evocative description of this function might be Distance Weighted Density. A good way to think about this would be to consider the value of Coffee Shops in the landscape. Being near one coffee shop is good, but being near two is twice as good. A simple way of modeling this would be with the Point Statistics function. The images below and their captions demonstrate the modeling doughnut shop accessibility using a focal sum approach and kernel density. Before looking at these functions, Take a look at the coffee_shops_2000 layer in the businesses group layer. Look at the attribute table and notice that each shop has a Weight which is set to a value of 1 for each shop.
Point Statistics (Focal Sum)
The point statistics function is very similar to the Focal Statistics function that was demonstrated earlier inb this tutorial. The differnce is that Point Statistics takes weighted points as inputs as opposed to a raster. The illustration below shows how Point Statiscics produces an output raster where the value of each cell is the count of points within the neighborhood.
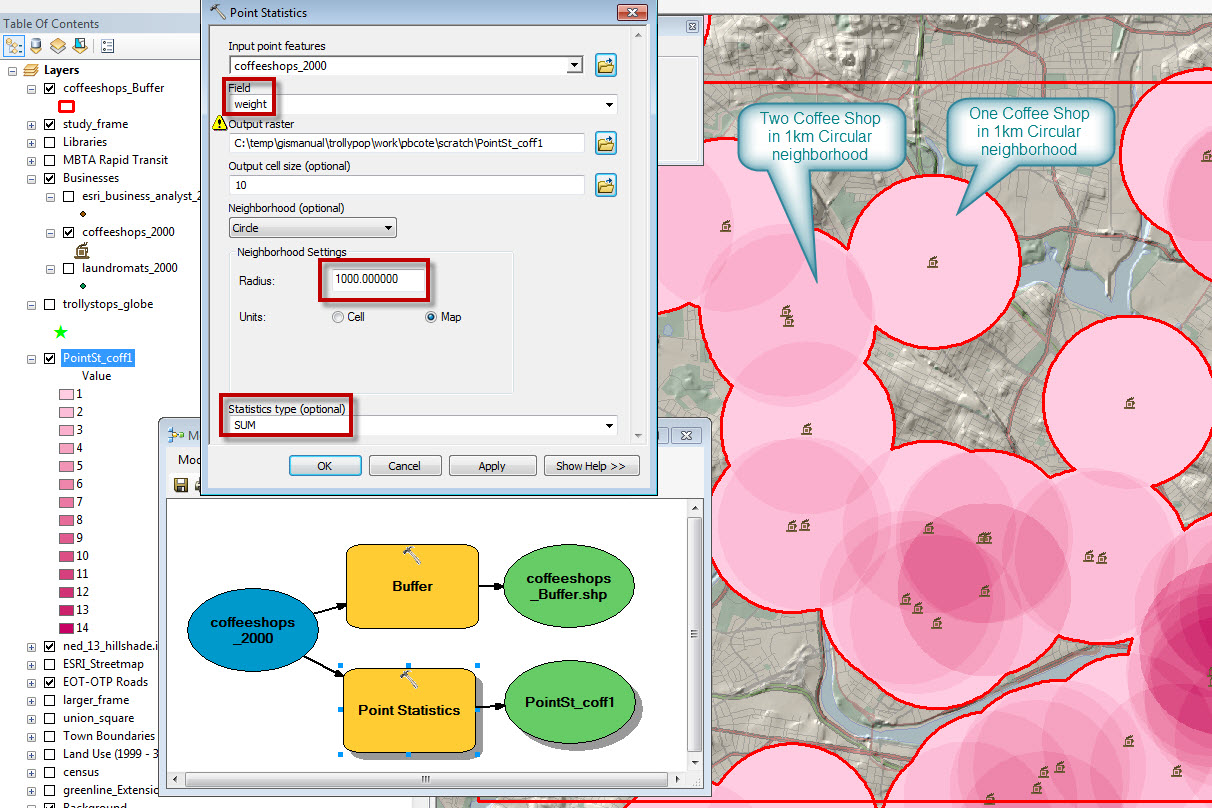
Note that you can change the weights and the statistics type to calculate the Mean or even Variety of vlues in the neighborhood.
Kernel Density
Consider the Treat-Seeker whoplaces a value of being at a swwetshop as 1. Being in the sdame location as twosweet shops as two. But the value of a sweet-shop falls to zero as the distance increases to 1 kilometer. At 500 meters away, the value a single sweet-shop is 0.5. Being 500 meters from two sweet-shops has a value of 1. The Kernel Density function (in Spatial Nalyst Tools > Density simulates this conceptual model of valuing sources cumlatively but diminishing with distance. The kernal Density function is often used to make Heat Maps. But you often see that analysts do not bother to include legends or interpret the results.
The odd thing is that the ESRI Kernel Density function can easily be interpreted with the limit is 1km. But it cannot be interpreted the same way with other settings. The slides below demonstrate how to interpret Kernel Density and how to normalize its results for limits other than 1km.
References
If the normalized Kerbnel Denisity function seems to do a good job of simulating the values of a treat seeker. Normalized kernel density results for facilities of different drop-off limits may be compared productively and even added together.
Note on slides 4 and 5, that this function does not consider mediating conditions like roads or water.
Editorial Comment: I believe that this function could be implemented with a more intuitive and easy-to-interpret option for normalizing density. In such a function,the density function wouls always be One, and the numerator, the number of points at or near the center of the search circle. With a function like this, the density values near a single point should be approximately 1, regardless of my search radius. The search radius should affect the steepness of the fall-off function which leaves you at zero near the limit of the search radius. This way you would be able to compare the values of kernel density for models that have different search radii. It would even be possible to add two rasters of this sort together win a meaningful way Listening ESRI?
It is actually possible to fix your kernel daneity results to have this normalized property by using the raster calculator or the divide function to divide the result by a number that seems to be a little more than the value of a cell on the raw kernel density result that is near a single solitary inpout point.
Cost Weighted Distance
You may recall in our discussion of Spatial Mechanisms that many of the ways that real thingsand conditions are related to eachother, for example, relationships of Exposure or Accessibility, involve a source and some related things and conditions, and in-between there is some mediating condition. To say this in different words, while many of our GIS functions simulate spatial mechanisms with simple radiating distances like Buffers, Euclidean Distance, and the Focal and Kernal Density functions described above. In the real world, it is almost always the case that sme intermediating condition, like wind, or the presentrse of roads, or slope makes somee places more connected to eachother than others. Relationships in the real world usually involve distance mediated by some cost.
If you look at the tools in the ArcGIS Distance Tool-Set you will find the familiar Euclidean Distance tool, and also a bunch of other distance tools that allow mediating conditions to be taken into account. Many of these distance tools allow for the preparation of a Cost Map which rates the cost of crossing each cell in terms of a Cost per Map Unit where the map units are the X-Y units of the projection you are using. IN our example data-set, our map units are meters.
References:
You will find a working CostDistance application in the pbcRasterDemo toolbox. Open it for editing and take a look at what each of the tools does. There are pretty extensive notes included in the model itself, Here are a few tips that may not be obvious.
- The Feature to Raster tool only takes integer fields to determine the new cell values. This is awkward, since the cost of crossing small cells is usually going to involve fractions. So plan to use a raster-calculator function later to reduce these values.
- Often the expression to be used in the Raster Calculator requires some High-School Algebra skills to fiure out. Converting Miles per Hour to Miuntes per Meter boils down to:
1 / (("%streets_mph.img%" * 1609.0 ) / 60) - The metadata for the USGS Land Use Land Cover Map is the classic Anderson Land Use Coding Scheme. Also found in the Sources/USGS folder.
- Any of the Distance functions can start with Points, Lines or Polygons or rasters as sources. If you use a raster as your source information, the Cost Distance is calculated from cells that have values into the NoData area of the raster.
Parting Thoughts
We started this tutorial by looking at how the Sample function allows us to take values from a raster surface and apply them to features in a point or polygon feature class. The last bunch of models demonstrate how you can take elemental spatial functions and mix them with existing map data and parameters to create surfaces that may or may not represnt useful spatial patterns. Through successive operations we can use these functions to examine how our values for certain types of relationships add up. These new maps can help use to see places of particularly special opportunities or risks oe costs. These maps can be used for planning interventions.
The image above illustrates how we can use out model to evaluate each of the existing library locations based on the director's conceptual model of the qualities of an ideal hub.


